Un sistema de coordenadas permite "etiquetar" los puntos de una variedad diferenciable mediante un conjunto de n-tuplas. Los casos más sencillos de sistemas de coordenadas se definen sobre el espacio euclídeo o "espacio plano", aunque también es posible construirlos sobre variedades con curvatura. Un sistema de coordenadas sobre una variedad  n-dimensional se representa como un par ordenado
n-dimensional se representa como un par ordenado  formado por un dominio
formado por un dominio  y una aplicación diferenciable
y una aplicación diferenciable  a un conjunto abierto de
a un conjunto abierto de 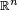 , éste último conjunto contiene los posibles valores de las coordenadas, que obviamente serán números reales.
, éste último conjunto contiene los posibles valores de las coordenadas, que obviamente serán números reales.
Sistema de coordenadas cartesianas
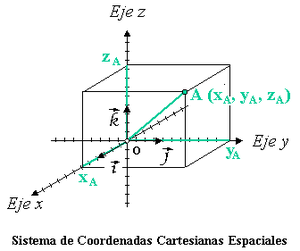
En un espacio euclídeo un sistema de coordenadas cartesianas se define por dos o tres ejes ortogonales igualmente escalados, dependiendo de si es un sistema bidimensional o tridimensional (análogamente en 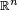 se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyección ortogonal del vector de posición de dicho punto (
se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyección ortogonal del vector de posición de dicho punto ( ) sobre un eje determinado:
) sobre un eje determinado:
Cada uno de los ejes está definido por un vector director y por el origen de coordenadas. Por ejemplo, el eje x está definido por el origen de coordenadas (O) y un versor (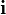 ) tal que:
) tal que:
 , cuyo módulo es
, cuyo módulo es  .
.
x_\text{A} = {\text{OA} \cdot \mathbf {i} \over |\text{OA}| \cdot |\mathbf{i}|} = El valor de la coordenada x de un punto es igual a la proyección ortogonal del vector de posición de dicho punto sobre el eje x.
Asi pues la coordenadas se establecen como las reglas de las matematicas unicas, dando asi la necesidad de utilizarlas y saber que los ejes X y Y respectivamente no tienen nada que ver con las coordenadas y son ya descartadas de la grafica.
Sistema de coordenadas polares
El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del plano se determina por un ángulo y una distancia.
Sistema de coordenadas cilíndricas
El sistema de coordenadas cilíndricas 0,\ 0\le \varphi< src="http://upload.wikimedia.org/math/2/6/9/269b0061681caba46512f1309fa4ea56.png"> se usa para representar los puntos de un espacio euclídeo tridimensional. Resulta especialmente útil en problemas con simetría axial. Este sistema de coordenadas es una generalización del sistema de coordenadas polares del plano euclídeo, al que se añade un tercer eje de referencia ortogonal a los otros dos. La primera coordenada es la distancia existente entre el eje Z y el punto, la segunda es el ángulo que forman el eje X y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada z que determina la altura del cilindro.
Sistema de coordenadas esféricas
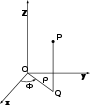
Al igual que las coordenadas cilíndricas, el sistema de coordenadas esféricas se usan en espacios euclídeos tridimensionales. Este sistema de coordenadas esféricas está formado por tres ejes mutuamente ortogonales que se cortan en el origen. La primera coordenada es la distancia entre el origen y el punto, siendo las otras dos los ángulos que es necesario girar para alcanzar la posición del punto.
Coordenadas geográficas
Este tipo de coordenadas cartográficas, subtipo de las coordenadas esféricas, se usa para definir puntos sobre una superficie esférica. Hay varios tipos de coordenadas geográficas. El sistema más clásico y conocido es el que emplea la latitud y la longitud, que pueden mostrase en los siguientes formatos:
- DD --- Decimal Degree (Grados Polares): ej. 49.500-123.500
- DM --- Degree:Minute (Grados:Minutos): ej. 49:30.0-123:30.0
- DMS -- Degree:Minute:Second (Grados:Minutos:Segundos): ej. 49:30:00-123:30:00
También se puede definir las coordenadas de un punto de la superficie de la Tierra, utilizando una proyección cartográfica. El sistema de coordenadas cartográficas proyectadas más habitual es el sistema de coordenadas UTM.
Coordenadas curvilíneas generales
Un sistema de coordenadas curvilíneos es la forma más general de parametrizar o etiquetar los puntos de un espacio localmente euclídeo o variedad diferenciable (globalmente el espacio puede ser euclídeo pero no necesariamente). Si tenemos un espacio localmente euclídeo M de dimensión m, podemos construir un sistema de coordenadas curvilíneo local en torno a un punto p siempre a partir de cualquier difeomorfismo que cumpla:
Para cualquier punto q cercano a p se definen sus coordenadas curvilíneas:
Si el espacio localmente euclídeo tiene la estructura de variedad de Riemann se pueden clasificar a ciertos sistemas de coordenadas curvilíneas en sistema de coordenadas ortogonales y cuando es sistema de coordenadas ortonormales. Las coordenadas cilíndricas y las coordenadas esféricas son casos particulares de sistemas de coordenadas ortogonales sobre el espacio euclídeo  .
.
Coordenadas curvilíneas ortogonales
Un sistema de coordenadas curvilíneas se llama ortogonal cuando el tensor métrico expresado en esas coordenadas tiene una forma diagonal. Cuando eso sucede muchas de las fórmulas del cálculo vectorial diferencial se pueden escribir de forma particularmente simple en esas coordenadas, pudiéndose aprovechar ese hecho cuando existe por ejemplo simetría axial, esférica o de otro tipo fácilmente representable en esas coordenadas curvilíneas ortogonales.
Las coordenadas esféricas y cilíndricas son casos particulares de coordenadas curvilíneas ortogonales.


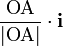





No hay comentarios:
Publicar un comentario