En física newtoniana, el campo gravitatorio es un campo vectorial conservativo cuyas líneas de campo son abiertas. Puede definirse como la fuerza por unidad de masa que experimentará una partícula puntual situada ante la presencia de una distribución de masa. Sus unidades son, por lo tanto, las de una aceleración, m s-2. Matemáticamente se puede definir el campo como ,
donde 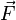 es la fuerza de gravedad experimentada por la partícula de masa m en presencia de un campo
es la fuerza de gravedad experimentada por la partícula de masa m en presencia de un campo  .
.
Ejemplos de campos gravitatorios
El campo  creado por una distribución de masa esférica, viene dado en cada punto fuera de la esfera por un campo vectorial que apunta hacia el centro de la esfera:
creado por una distribución de masa esférica, viene dado en cada punto fuera de la esfera por un campo vectorial que apunta hacia el centro de la esfera:
(1)
,
donde r es la distancia radial al centro de la distribución. En el interior de la esfera central el campo varía según una ley dependiente de la distribución de masa (para una esfera uniforme, crece en forma lineal desde el centro hasta el radio exterior de la esfera). La ecuación (), por tanto, sólo es válida a partir de la superficie exterior que limita el cuerpo que provoca el campo, punto a partir del cual el campo decrece según la ley de la inversa del cuadrado. El campo  creado por una distribución de masa totalmente general en un punto del espacio
creado por una distribución de masa totalmente general en un punto del espacio  :
:
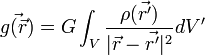 ,
,
El interés de realizar una descripción de la interacción gravitatoria por medio de un campo radica en la posibilidad de poder expresar la interacción gravitacional como el producto de dos términos, uno que depende del valor local del campo  y otro, una propiedad escalar que representa la respuesta del objeto que sufre la acción del campo. Por ejemplo, el movimiento de un planeta se puede describir como el movimiento orbital del planeta en presencia de un campo gravitatorio creado por el Sol.
y otro, una propiedad escalar que representa la respuesta del objeto que sufre la acción del campo. Por ejemplo, el movimiento de un planeta se puede describir como el movimiento orbital del planeta en presencia de un campo gravitatorio creado por el Sol.
Los campos gravitatorios son aditivos; el campo gravitatorio creado por una distribución de masa es igual a la suma de los campos creados por sus diferentes elementos. El campo gravitatorio del Sistema Solar es el creado por el Sol, Júpiter y los demás planetas.
Líneas de fuerza
Una línea de fuerza o línea de flujo, normalmente en el contexto del electromagnetismo, es la curva cuya tangente proporciona la dirección del campo en ese punto. Como resultado, también es perpendicular a las líneas equipotenciales en la dirección convencional de mayor a menor potencial. Suponen una forma útil de esquematizar gráficamente un campo, aunque son imaginarias y no tienen presencia física.
Potencial gravitatorio
La naturaleza conservativa del campo permite definir una magnitud, que se podría llamar energía mecánica, tal que la suma de la energía potencial y energía cinética del sistema es una cantidad constante. Esto implica que el trabajo realizado en el seno de un campo gravitatorio dependerá sólo de las posiciones final e inicial, y no de la trayectoria seguida (así,el trabajo realizado a lo largo de una supericie cerrada será nulo). Así a cada punto del espacio se le puede asignar un potencial Φ gravitatorio relacionado con la densidad de la distribución de masa y con el vector de campo gravitatorio por:
Podemos demostrar matemáticamente de forma sencilla (y esto es extensible al campo eléctrico), que efectivamente el campo gravitatorio de la mecánica newtoniana es conservativo: Primero deberíamos notar un hecho matemático importante, y es que si un campo vectorial  se puede expresar como gradiente de algún campo escalar
se puede expresar como gradiente de algún campo escalar 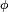 , es decir, si
, es decir, si  entonces el trabajo realizado a lo largo de cualquier trayectoria depende sólo del estado final y el inicial. La función escalar
entonces el trabajo realizado a lo largo de cualquier trayectoria depende sólo del estado final y el inicial. La función escalar 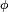 se llama función potencial del campo vectorial
se llama función potencial del campo vectorial  . Para probar esto hay que integrar la fuerza a lo largo de una determinada curva
. Para probar esto hay que integrar la fuerza a lo largo de una determinada curva  , es decir, debe calcularse la integral de línea:
, es decir, debe calcularse la integral de línea:
(*)
que, si  y
y  son los puntos en el espacio tridimensional con que empieza y acaba C respectivamente, y se designamos la función
son los puntos en el espacio tridimensional con que empieza y acaba C respectivamente, y se designamos la función  nos quedará
nos quedará
Llamando  y
y  . Ahora, partiendo de () ahora tenemos que
. Ahora, partiendo de () ahora tenemos que
que con una simple inspección concluimos que es:
Ahora obtenemos pues  . El escalar − φ(x) se llama energía potencial en x, y vemos que su suma con el escalar k(x) tiene que mantenerse constante, ha de ser la misma. En el caso del campo gravitatorio,tenemos que
. El escalar − φ(x) se llama energía potencial en x, y vemos que su suma con el escalar k(x) tiene que mantenerse constante, ha de ser la misma. En el caso del campo gravitatorio,tenemos que
con r = (x2 + y2 + z2)1 / 2. El vector unitario de dirección puede ser puesto  , así que:
, así que:
Y este campo de fuerza es obviamente un gradiente de  ,que es la función potencial. Con esto queda pues demostrado que el campo gravitatorio es conservativo (la energía mecánica, en ausencia de otras fuerzas externas, ha de conservarse). La demostración para el caso del campo eléctrico es análoga con pocos matices (la fuerza puede ser atractiva o repulsiva, y cargas iguales se reepelen, mientras que en el campo gravitatorio sólo hay atracción).
,que es la función potencial. Con esto queda pues demostrado que el campo gravitatorio es conservativo (la energía mecánica, en ausencia de otras fuerzas externas, ha de conservarse). La demostración para el caso del campo eléctrico es análoga con pocos matices (la fuerza puede ser atractiva o repulsiva, y cargas iguales se reepelen, mientras que en el campo gravitatorio sólo hay atracción).





![W=\int_{C}F(x,y,z)d\alpha = \int_{t_a}^{t_b} \nabla \phi[\alpha(t)]\alpha^{\prime}(t)dt = \phi[\mathbf{r}(t_b)]-\phi[\mathbf{r}(t_a)]= \phi(\mathbf{r}_2)-\phi(\mathbf{r}_1)](http://upload.wikimedia.org/math/2/d/e/2dea109f867846b7dd40486ca3b4d3bb.png)
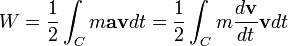
![W=\dfrac{m}{2}[\mathbf{v}^{2}(t_b)-\mathbf{v}^{2}(t_a)]= k(\mathbf{r}(t_a))-k(\mathbf{r}(t_b))](http://upload.wikimedia.org/math/e/8/f/e8f86441fe515ae9df6a5c4b375f134b.png)


No hay comentarios:
Publicar un comentario